Particle Size Distribution
Soils

Using Laser Diffraction in Folk and Ward Phi Notation

Soil Granulometry Application Note

Abstract

This application note is for geologists, environmentalists,
petroleum engineers, and others who use soil granulometry
as one important parameter for their studies. It demonstrates
an example of how the Beckman Coulter LS 13 320
can be applied to granulometry. An academic team used
the LS 13 320 to understand the deposition of soil
sediments in a Northwestern Chinese mountain range.

Introduction

Soil studies span a range of applications including agriculture,
architectural planning, and historical environmental studies3
.
Characterization of soils by particle size distribution
gives major insight into the deposition history of the sample.
Grain size is one of the indicators to understand how
soil formed (e.g., fluvial or loess deposits4,5). Fluvial
deposits are created from flowing water, including rivers
or streams, while loess deposits form from wind-blown
silt particles. Sedimentation rate6,7 and sieve analysis7
are two examples of the tools traditionally utilized
to determine size distribution of soils. Traditional methods
are time-consuming; they each have bias, mostly related
to the particles’ shape. Moreover, they require additional
tedious calculations to present the results in Phi notation.
None of these methods is a direct measurement of soil
particle size; all measure a property that is, at best,
tangentially related to particle size. Laser diffraction is a
superior option for soil sizing7,8. Worldwide, Beckman
Coulter laser diffraction instruments are successfully
applied in industry and academic research, obtaining
close correlation with earlier methods in sizing soils8
.
The latest instrument in the series, the LS 13 320,
yields highly reproducible results—and extremely fast
analysis—in Phi notation in a few seconds.

Study Background

Soil samples from the Bogda Mountains in Northwest
China were analyzed on the LS 13 320. The results
were presented by the Department of Geological Sciences and Engineering, Missouri University of Science
and Technology (MST). The data were part of a study
of mixed fluvial and loess deposits in an intra-continental
rift basin, the Mid-Permian Quanzijie Low-Order Cycle.
The Beckman Coulter Particle Characterization applications
scientists generated the data in collaboration with MST.
LS 13 320 results supported preliminary interpretation,
in support of the hypothesis that massive mudrock of
the Quanzijie (QZJ) Formation are loess deposits of an
eolian (wind-deposited) origin9
. Thirty-one samples
from the QZJ were analyzed with the LS 13 320 at various
locations throughout the basin (Lower, Middle, and Upper).
Interestingly, grain size remained roughly homogenous for
all samples regardless of lithocolumn (solid depth) location
(Figures 1–3). This is consistent with characteristics of
wind-deposited materials.

Method

• In 150 mL beakers, one mL of 1M HCL was added
  to ~130 mg of each of the samples to loosen and
  disperse the soils.
• Approximately 60 mL of DI water and one mL of
  10% calgon were added and probe-sonicated for
  four minutes at 100 W. The preparation beaker
  was placed into a 500 mL beaker with water to
  prevent boiling by prolonged sonication.
• The entire content was added and rinsed into the
  LS 13 320 Aqueous Liquid Module (ALM) and run
  with a standard SOP

Results were reported using Folk & Ward Phi statistics
and graphs.

Conclusion

The LS 13 320 played a vital role in understanding the
mechanisms of deposition for soil samples in a Chinese
mountain range. The methods presented here have
frequently been used around the world in peer-reviewed
research publications—such as those presented in the
References section—as well as in private industry

Particle Size Distribution
Cement

Critical Particle Size Distribution for Cement using Laser Diffraction

“London Bridge is falling down….” Well not really, but only because the cement is still doing its good work! Producing high performance cement is directly related to maintaining a very specific Particle Size Distribution. Traditional size characterization methods include: Sieving using a 45μm sieve screen, Blaine Number measurement, and the Wagner turbidimeter measurement. These methods yield only a single number and are not sufficient to adequately characterize the crucial particle size distribution (PSD) of cement. Laser Diffraction is quickly becoming the method of choice as it yields a clear and accurate picture of the entire PSD.

Introduction

To say that the cement industry is big business may be the understatement of the decade! In 2014, the global cement production was approximately 4.2 billion metric tons¹. Consider just the number of buildings, bridges, and roads that are built around the world every year using cement and you begin to get an idea of the magnitude of safety and quality considerations associated with its everyday use.
It is quite common to confuse cement with concrete, but in actuality, cement is a construction material used to produce concrete. There are many stages within the cement production process that require particle size characterization. Figure 1 below illustrates a typical cement production process. The most important point in the process to perform a Particle Size Distribution measurement is at the final product stage. The largest contribution to cement strength comes from particles smaller than 30μm, while particles smaller than 10μm contribute to the early curing stage and particles between 10-30μm have a larger impact at the later stage in the hardening process2. Generally speaking the larger the distribution percentage of particles between 3-30μm, the better the quality of the cement². Experience tell us that the optimal size distribution is when 60-70% of particles in the overall distribution are within the range of 3-30μm and 10-20% are smaller than 3μm². In the grinding process, overgrinding creates unnecessary costs; additionally it creates too many particles smaller than 3μm². This phenomenon, in turn will produces too much heat during solidification, causes over sedimentation, which can further lead to quality issues like cracking. On the other hand, under-grinding will result in too many larger particles that in turn will prolong solidification time and can reduce overall strength.

Laser diffraction has emerged as the preferred sizing method in cement industry due to its simplicity and accuracy as compared to the more traditional methods. Current laser diffraction users in cement industry have witnessed good correlation between wet (alcohol) or dry analysis using the Beckman Coulter Dry Powder System (Tornado™) This is illustrated clearly in the “Measurement of Particle Size Distribution in Portland Cement Powder: Analysis of ASTM Round Robin Studies: technical paper.

Results and Conclusions

To standardise characterisation of cement products using laser diffraction, NIST has issued a standard reference material (SRM) of Portland cement (NIST SRM 114q). In addition to listing the certified specific surface area values from Blaine and Wagner measurements and certified sieve residue values, the Particle Size Distribution of NIST SRM 114q is also specified using laser diffraction, both wet and dry analyses as the measurement techniques3. Beckman Coulter did not participate in the round robin analysis that determined the NIST SRM 114q size distribution. Fig. 2 details the analysis results of using a Beckman Coulter LS 13320 XR to characterize the NIST SRM 114q, both using both wet and dry methods. In the Certificate of Analysis, NIST specifies Simultaneous 95% Expanded Uncertainties for the Difference between a typical Laboratory and the Certified Value of SRM 114q3. The boundaries for the normal agreement are marked by two blue solid lines in Fig. 2 and the boundaries for the tighter agreement are marked by error bars at each data point in Fig. 2. As the graph clearly illustrates in Figure 2, both LS 13320 wet (Using the ULM module) and dry (using the Tornado Dry Powder System module) analyses resulted in excellent agreement, all well within the tighter limits, required by the NIST certification².

References

• 1. US and World Cement Production 2014 Retrieved from http://www.statista.com/statistics/219343/cement-production- worldwide/
• 2. Guillermo Smart, AN-12784A BCPCS009LE LS-Cement
• 3. Chiara F. Ferraris, Vincent A. Hackley, and Ana Ivelisse Avil´es Measurement of Particle Size Distribution in Portland Cement Powder: Analysis of ASTM Round Robin Studies.
  Retrieved from http://fire.nist.gov/bfrlpubs/build04/PDF/b04040.pdf

Particle Size Distribution
Pigments

Using Laser Diffraction Analysis in Pigment Sizing

Introduction

Pigments and paints are an important class of industrial
materials. They play an important role and
can be found in everyone’s lives. From cosmetics to
car paint, from household paint to the ink in the
humble ballpoint pen or the ubiquitous inkjet printer,
nobody today will fail to encounter a wide variety
of pigments and paints in their daily routine.

The application properties of a given pigment/
paint system are determined largely by the particle
size distribution of the pigment particles. Particle size
determines the tinctorial strength or the depth of
color (neglecting self-scattering of the pigment);
additionally, it may also be an important physical
parameter of the pigment system itself. For example,
in printing inks, it is important that the ink particles
are not larger than the nozzle delivery system that
dispenses the ink.

The ability of a given pigment to absorb light
(tinctorial strength) increases with decreasing particle
diameter, and accordingly increased surface
area, until it reaches a point when the particles become
translucent to the incident light. This one factor alone
makes the measurement of particle size critical to
the performance for many of today’s pigment applications.

The LS™ Series multi-wavelength particle size
analyzers from Beckman Coulter, Inc. utilize a complementary
scattering technology for the sizing of
sub-micron particles. This technical note describes, by
reference to real samples, how pigment particles are
sized using the PIDS™ system (Figure 1).

Sizing pigments using laser diffraction analysis

A variety of particle sizing technologies have been
employed to measure the particle size distributions
of pigment systems. But, laser diffraction has
increasingly become the most commonly employed
technique in the determination of particle size distributions.
The acceptance of the technique stems from
its ease of use and the varied ways that samples can
be presented to the system for analysis.

A sample of interest is illuminated by laser light
of a given wavelength. The technique relies upon
the fact that the particles will scatter light when
exposed to electromagnetic radiation. The resulting
scattering pattern can be measured electronically
and then deconvulated mathematically to infer a
particle size distribution.

The ease of use coupled with a short analysis
time, typically less than one minute, has made laser
diffraction, as stated earlier, the primary method by
many companies for process control. However, there
is a drawback: a majority of pigment systems are
sub-micron in nature and this is the size range where
standard laser diffraction instruments have typically
struggled to provide accurate information.

It is important to first understand why laser diffraction
particle size analyzers have difficulties sizing
sub-micron materials. When illuminated by a
laser beam, large particles scatter light strongly at
small angles and with readily detectable maxima
and minima in the scattering pattern. This means
that detectors placed at small angles, relative to the
optical path and with sufficient angular resolution,
can detect the fine detail in the scattering pattern.
It is the accurate measurement of these maxima
and minima that allows the determination of the
mean size of the material being analyzed and the
width and detail of the distribution.

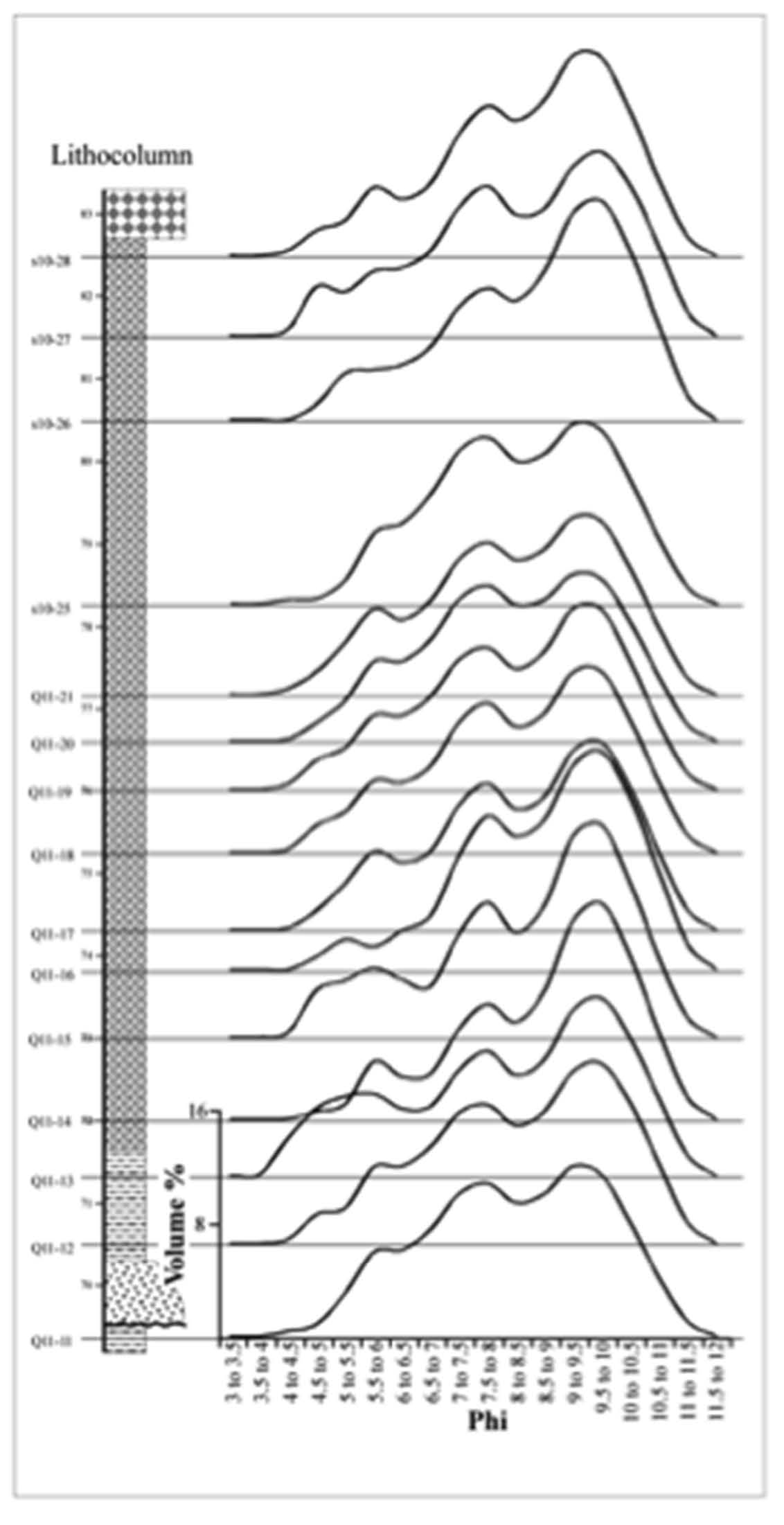
Conversely, small particles scatter light weakly
and without any discernible maxima and minima
until high angles of measurement are reached. As
can be seen in Figure 2, once there are particles
below 1 μm, many difficulties in the measurment
are encountered with weak scattering signals.

Different manufacturers have adopted different
solutions to overcome these limitations with varying
degrees of success. Most early efforts have focused
on the measurement of back-scattered light, and
indeed some manufacturers continue to pursue this
approach. In the early 1990s, Beckman Coulter
devised a novel technique for enhancing sub-micron
sizing in standard laser diffraction systems. This
involved the utilization of additional wavelengths
apart from the main diffraction laser source. The
technique is called PIDS,™ for Polarization Intensity
Differential Scattering.

PIDS

The technology employed in PIDS is simple and takes
advantage of the well-established and understood
Mie theory of light scattering.

PIDS (Polarization Intensity Diferential
Scattering) relies upon the transverse nature of light,
i.e., it consists of a magnetic vector and an electric
vector at 90 degrees to it. If, for example, the electric
vector is “up and down,” the light is said to be
vertically polarized.

When we illuminate a sample with light of a
given wavelength and polarization, the electric field
establishes a dipole. The oscillations of the electrons
in this dipole will be in the same plane of
polarization as the propagated light source. The
oscillating dipoles in the particles radiate light in all
directions except that of the irradiating light source.

PIDS takes advantage of this phenomenon. Three
wavelengths – 450 nm, 600 nm, and 900 nm –
sequentially illuminate the sample, first with vertically
and then horizontally polarized light. The
scattered or re-radiated light from the sample is
then measured over a range of angles. By analyzing
the differences between the horizontally and the vertically
polarized light for each wavelength, we can
gain information about the particle size distribution
of the sample. It is important to remember that we
are measuring the differences between the vertically
and the horizontally polarized signals, and not simply
the values at a given polarization.

The intensity vs. scattering angle information
from the PIDS signals is then incorporated into
the LS algorithm from the intensity vs. scattering
angle data from the primary laser, giving a continuous
size distribution, 0.04 μm to 2,000 μm
(Beckman Coulter LS™ 230 and LS 13 320).

The technique has proven to be extremely accurate
for the sizing of both spherical and non-spherical
sub-micron particles.

Other manufacturers have begun to utilize
multi-frequency wavelength analysis for sub-micron
analysis, typically using just one additional wavelength,
though they do not adopt the same approach
as is taken for PIDS.™ While providing extra data, it
does not offer the same amount or level of detailed
information that is offered by PIDS technology. The
extra wavelength is normally provided by a blue
light source with a wavelength of approximately
460 nm. By shortening the wavelength, gains are
made by primarily ensuring a larger light flux signal
is generated compared to the standard laser light
source, thereby making its quantification easier.
Secondly, by using a shorter wavelength, the difference
between the small particles are minimalized, in
terms of size and the wavelength of the illuminated
light source; this is an important parameter for standard
diffraction analysis. Diffraction data, in effect,
stops being meaningful as particles get smaller in
relation to the wavelength that is irradiating them.

The Problem with Pigments

,p>Pigments provide a unique problem not encountered
with most materials that are measured using laser
diffraction instruments. The vast majority of samples
measured on commercially available instruments
are not colored and this makes their analysis more
straightforward. It is important to consider why this
is the case. For an accurate particle size to be calculated,
both the real refractive index of the material
and its imaginary component must be known. This
becomes more important for small particles as the
mathematical treatment to successfully size them
becomes the more rigorous Mie theory.

While the real refractive index is a value that is
well understood by the majority of analysts, the
imaginary component is less so. It is, in fact, the
degree of absorbance that is exhibited by the sample
at a given wavelength. Non-colored materials exhibit a
fairly uniform absorbence across the ultra violet/
visible (UV/Vis) electromagnetic spectrum.

Pigments, however, provide an entirely different
challenge. The reason they are colored lies with the
fact that they absorb certain wavelengths preferentially.
This must be taken into account when calculating
the particle size distribution, particularly if the
particles are small. For example, how will a blue
pigment with an absorbance maximum at 630 nm
interact with a helium neon laser (wavelength
633 nm), which is the choice of a number of manufacturers
for their primary laser light source? The material essentially behaves as a black body, which
must be taken into account during optical modeling.
Failure to do so will lead to significant errors that
will increase with a decrease in particle size.

The real refractive index remains an important
function and can be either calculated or estimated
from known constants, and any error associated
with this can be minimized.

Thus, it is easy to see that the quantification of
the imaginary component of the complex refractive
index is extremely important for the accurate determination
of pigment particulate systems.

Determining the Imaginary
Component

The determination of the imaginary component of a
pigment is a relatively straightforward measurement.
It is achieved using a UV/Vis spectrophotometer,
which measures the relative absorbency of a material
per given wavelength. It is this preferential absorbtion
that dictates the color of a material.

Two things must be taken into account: first,
one must ensure that no large particles are present
in the spectrophotometer sample cell, as they will
give rise to forward scatter and will “blind” the
detector, compromising the absorbance measurement.
It may be necessary to filter a sample to remove large
particles; particles should be no bigger than a few
microns.

Second, the relative amount of absorbtion must
be taken into account in the calculation of the optical
model. This will not be a constant and will need to
be determined for each type of instrument. Once this
has been done, these values can then be used when
calculating optical models for a given pigment.

In terms of the allowance used for the imaginary
component, the approach taken for each complementary
wavelength needs to be fully evaluated.
A novel approach related to the obscuration value,
which is associated directly with the amount of
sample in the analyzer, can be employed. A more
sophisticated method would be to use Beer’s Law.
However, one would need to know the exact concentration
of the solution. But, absorbencies taken
at a specific concentration could then be directly
related to one another. The more quantitative
approach would be to determine the exact concentration
of the solution.

Each manufacturer takes a different approach to
the calculation of optical models. Beckman Coulter
allows users to calculate a complete Mie theory optical
model for a given sample. The optical model can be
generated with the latest version of software in as
little as three seconds.

Using Complementary Information

When analyzing pigments, it is also beneficial to
utilize other sources of information to initially verify
or confirm the results obtained. Once correlating
information has proven the suitability of a given
model for a particular sample it can then be used
with confidence for that material. The best sources
of correlating information are photomicrographs.
These can be images from simple microscopes to
electron microscopes. This approach is particularly
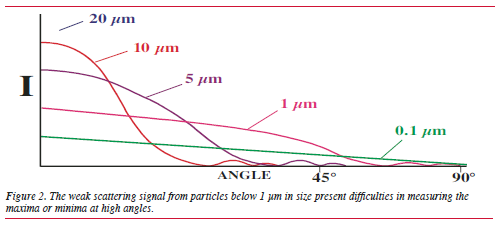
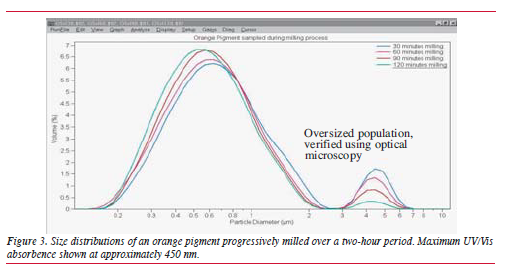
important for the detection of small amounts of oversized
materials. This can be a common problem with
many pigment systems due to the type of size reduction
or milling techniques utilized. Ball mills can give
rise to small amounts of oversized materials that may
remain undetected by laser diffraction, particularly
if the imaginary component of the refractive index
is not taken into account.

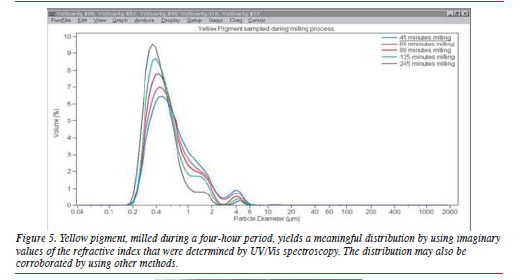
Beckman Coulter, working in conjunction with
a selected number of pigment manufacturers, has now
gained valuable experience in the particle size
analysis of many different pigment systems. The
applicability of an optical model for a given pigment
is best determined if one tracks a milling process over
time. If the correct refractive index values have been
used to create the optical model, one should obtain
a constant reduction of the mean size.

The Question of Shape

A criticism leveled at all laser-based particle sizing
devices is that they make no allowance for the shape
of the materials under test, regardless of the size of
the particles. The reasons for this lie with the underlying
assumptions, used in calculating size distributions
from the raw data generated during the analysis.

The mathematical models used to calculate distributions
are based on scattering of light by a
sphere. So any reported distribution is, in effect, an
equivalent spherical distribution of the material being
analyzed. In most instances this is quite adequate
since most particles approximate to a spherical system
adequately enough.

Particles in milled pigments will not be perfect
spheres, so how does this affect their recovered
sizes using the technique described above? The
ideal way to evaluate this is with reference to
known standards.

Until recently, sourcing suitable sub-micron,
non-spherical particles for studies of this type has
been difficult because of the lack of independently
produced and assayed materials. However, the colloid
chemistry department at the University of
Utrecht now produces a variety of mono-dispersed,
non-spherical materials. Figure 6 shows the results
obtained for the analysis of sub-micron hematite
spindles (spheroids).

The size of the particles (determined by SEM,
or scanning electron microscopy) is 46.9 nm in
width and 130.8 nm in length, giving them an
approximate aspect ratio of 3:1. The particles are
mono-sized and are readily dispersed.

LS™ Series Particle Size

Distribution for Hematite spindles
The optical properties of the hematite spindles have
been determined from UV/Vis spectroscopy for the
imaginary component of the refractive index and
from UV/Vis spectroscopic ellipsometry data for the
real component. Using hematite has an added benefit,
in that being a colored material it mimics a pigmented
material well.

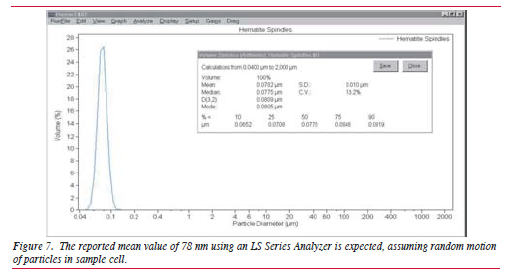
The reported value for the mean size from the
LS Series Analyzer is 78 nm (Figure 7), which is
well with in the range of what one would expect
given the random motion of the particles in the sample
cell. Statistically, one would expect the reported mean
size to be a function of all the possible orientations
of the particles as they traverse through the illuminated
beam. Indeed, instruments are designed to
ensure that particles in the sample cell are orientated
in a random manner with regard to their morphology
or shape.

Summary

If the right approach is taken, enhanced multi-frequency
laser diffraction can be employed successfully
to size particulate pigment systems.

For pigments, steps can be taken to determine
the imaginary component of the optical model for
laser diffraction particle size analyzer. It is also
worthwhile considering using other techniques to
initially corroborate the results obtained.